Annulus
An annulus (meaning little ring in Latin) is a ring-shaped figure between two concentric circles. Below are two examples. Think of an annulus as a circle with a concentric hole in it.

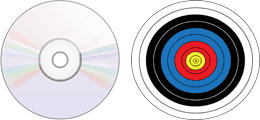
An annulus is something you've probably seen in your everyday life. The face of a CD or the colored rings on an archery target are two examples of objects that form a set of annuli.
Area of an annulus
The area of an annulus is
A = π(R2 - r2)
Where R is the radius of the outer circle and r is the radius of the inner circle.
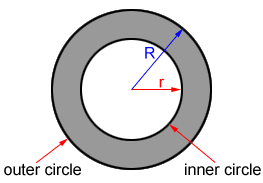
The area, A, of the annulus shown in gray can be found by subtracting the area of the circle, πr2, from the area of the outer circle, πR2. Therefore,
A = πR2 - πr2 = π(R2 - r2)
If the diameters of the annulus are given, the area of an annulus is
Where D is the diameter of the outer circle and d is the diameter of the inner circle.
Example:
What is the area of a cross section (the annulus) of a cylindrical concrete water pipe with the following dimensions?
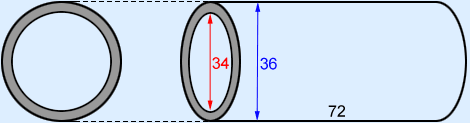
The area of the annulus is:
| A = | |
| = | |
| = | 35π |
Multiplying the area of the cross section by the pipe's length yields the volume, V, of concrete it would take to produce the pipe.
V = 35π × 72 = 2520π
