Heptagon
A heptagon is a polygon that has seven sides (Hepta- means seven) and seven interior angles. A heptagon is also sometimes called a septagon.
What is a heptagon
A heptagon is defined as a 7-sided, closed, two-dimensional shape. Heptagons are present in real life. Two real-life heptagon examples include the fifty pence and twenty pence coins in the UK.
Heptagon shape
The figure below shows a few examples of the shapes that a heptagon can take on.

Heptagon types
Heptagons are classified as regular or irregular and concave or convex.
Regular heptagon
A regular heptagon is a heptagon whose sides and interior angles are all equal in measure. The figure below shows a regular heptagon example:

Properties of a regular heptagon
A regular heptagon has the following properties:
- 7 interior angles measuring ~128.57° each.
- 7 exterior angles measuring 51.43° each.
- 7 congruent vertices
- 7 congruent sides
- 7 lines of symmetry
- Always convex.
Irregular heptagon
An irregular heptagon is a heptagon that has varying measures of sides and interior angles. The figure below shows an irregular heptagon example:

As can be seen in the figure, not all of the sides and angles of the heptagon are congruent, so it is irregular. An irregular heptagon can be either concave or convex.
Convex heptagon
A convex heptagon is a heptagon in which all interior angles measure less than 180°. As a result, all of the diagonals of a convex hexagon lie within the boundaries of the shape. A regular heptagon is always a convex heptagon, but a convex heptagon can either be regular or irregular. The figure below shows an irregular convex heptagon example.

Notice that none of the interior angles measure greater than 180°, but at the same time, the sides and interior angles are not all congruent.
Concave heptagon
A concave heptagon is a heptagon in which at least one interior angle measures greater than 180°. For any interior angle that measures greater than 180°, there is also a corresponding diagonal that will lie outside of the boundaries of the heptagon. Because at least 1 angle of the heptagon must me greater than 180°, but not all can equal 180° (since the interior angles of a heptagon always sum to 900°), all concave heptagons are irregular. The figure below shows a concave heptagon example:

Notice that two of the interior angles measure greater than 180°, so the heptagon is concave.
Heptagon properties
The following are properties of all heptagons:
- 7 sides, angles, and vertices.
- 7 interior angles that sum to 900°.
- 7 exterior angles that sum to 360°
- Can be divided into 5 triangles.
- Has 14 diagonals.
Heptagon formulas
Below are formulas for finding the area, perimeter, measure of the interior angles, and sum of the interior angles of a heptagon.
Heptagon area
The formula for the area of a regular heptagon is:
where a is the length of the side. This formula simplifies to approximately:
Perimeter of a heptagon
The regular heptagon perimeter formula is
where a is the side of the heptagon.
The perimeter formula for an irregular heptagon is simply the sum of each of its sides.
Heptagon interior angle formula
The formula to find the measure of the interior angles of any regular polygon is
where n is the number of sides in the polygon. Thus, for a regular heptagon:
Heptagon sum of interior angles formula
The formula to find the sum of the interior angles of any polygon is
where n is the number of sides. For a heptagon:
Heptagon angles
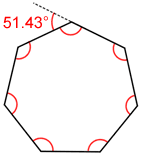
The sum of the interior angles of a heptagon is 900° and the sum of the exterior angles is 360°. For irregular heptagons, the individual interior and exterior angle measures will vary. For a regular heptagon, each of the seven interior angles measures ~128.57°.
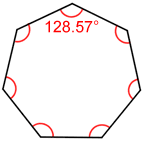
Each of the exterior angles measures ~51.43°.
Diagonals of heptagon
A diagonal is a line segment joining two non-consecutive vertices. A total of fourteen distinct diagonals can be drawn for a heptagon. The following figure is an example.
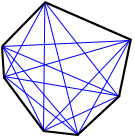
There are 4 diagonals extending from each of the 7 vertices of the heptagon above creating a total of 14 diagonals.
Interior angles of a heptagon
The sum of the interior angles of a heptagon equals 900°.
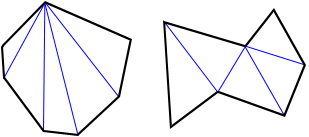
As shown in the figure above, four diagonals can be drawn to divide the heptagon into five triangles. The blue lines above show just one way to divide the heptagon into triangles; there are others. The sum of interior angles of the five triangles equals the sum of interior angles of the heptagon. Since the sum of the interior angles of a triangle is 180°, the sum of the interior angles of the heptagon is 5 × 180° = 900°.
Heptagon symmetry
A regular heptagon has 7 lines of symmetry and a rotational symmetry of order 7, meaning that it can be rotated in such a way that it will look the same as the original shape 7 times in 360°.
| Lines of symmetry | Rotational symmetry |
|---|---|
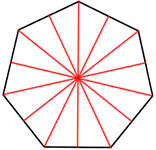 |
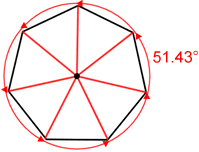 |
| 7 lines of symmetry | Seven 51.43-degree angles of rotation about the center |
