Ellipsoid
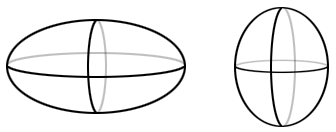
An ellipsoid is a 3D geometric figure that has an elliptical shape. It can be viewed as a stretched sphere. An ellipsoid gets its name from an ellipse. Any plane that cuts through an ellipsoid forms an ellipse. Two ellipsoids are shown in the figure below. Real life examples of an ellipsoid include an egg or a blimp.
Ellipsoid equation
The standard equation of an ellipsoid in the 3D coordinate system is
where a, b, and c are the lengths of the semi-axes of the ellipsoid.
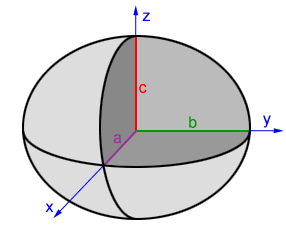
Types of ellipsoids
Ellipsoids are often classified based on the lengths of their semi-axes, a, b, and c. An ellipsoid has three axes of rotational symmetry. If an ellipsoid is rotated 180° (half a turn) about its axes, it will look the same as the original shape. The three axes are perpendicular to each other and they intersect at one point, called the center of the ellipsoid. The line segment from the center of the ellipsoid to the point where the axes intersect with the surface is called a semi-axis. The lengths of the semi-axes are often represented by a, b, and c as shown in the figure below.
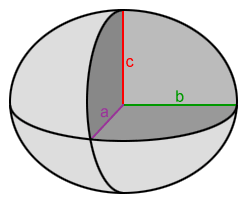
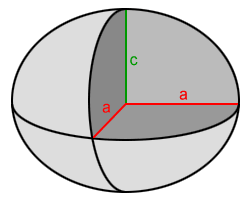
If a≠b≠c, we just called it an ellipsoid. If two of the three semi-axes are equal in length, as in a=b and a≠c, we call the ellipsoid an oblate spheroid or a prolate spheroid. Oblate spheroids have a shorter third semi-axis and a prolate spheroid has a longer third semi-axis as compared to the length of the two equal semi-axes.
| Oblate spheroid | Prolate spheroid |
|---|---|
 |
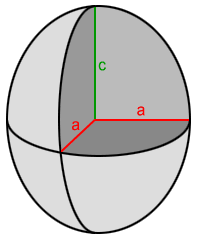 |
| a=b and a>c | a=b and c>a |
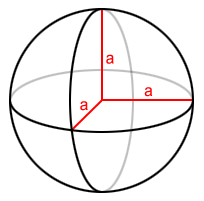
Sphere
A sphere is a special case of an ellipsoid in which a = b = c.