Spiral
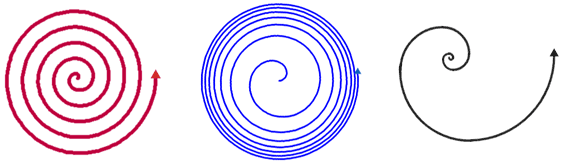
A 2D spiral is an open curve that revolves around a fixed central point, called the center, that moves farther away from the center as it revolves. Below are three different types of spirals.
Spirals exist in nature and man-made objects. The spiral galaxy and a seashell shown in the first two figures below are spiral shaped. The staircase is also in the shape of a spiral.

The archimedian spiral and golden spiral are two well known 2D spirals.
Archimedian spiral
In polar coordinate form, the equation of the Archimedian spiral is r = θ, where r is the radius of a circle and θ is an angle in standard position. For each point graphed on the Archimedian spiral in the polar coordinate plane, the length of any radius of a concentric circle equals the angle measure in standard position.
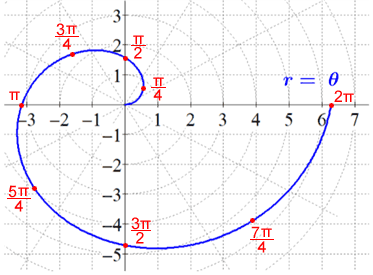
Several red points are graphed in the polar coordinate plane from 0 to 2π for the Archimedian spiral above. Connecting the points with a "smooth" curve creates a rotation of the spiral as shown above.
Golden spiral
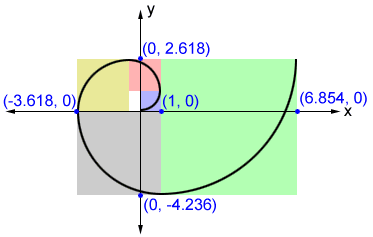
The golden spiral is a spiral that exhibits logarithmic growth. For every quarter turn, the golden spiral gets wider by a factor of the Golden ratio, φ=≈1.618.
The Golden spiral can be approximated using progressively larger golden rectangles partitioned into squares and similar golden rectangles, as shown in the figure below. The spiral is formed by connecting the corners of the successive squares with quarter circles.
3D spiral
In 3D, a spiral is an open curve that rotates around and along a line, called its axis.
3D spiral equation
The spiral shown below is a type of spiral referred to as a helix, and has a parametric equation of the form x(t) = rcos(t), y(t) = rsin(t), z(t) = at, where a and r are constants.
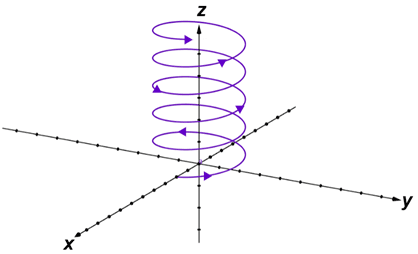
A helix can be traced over the surface of a cylinder.
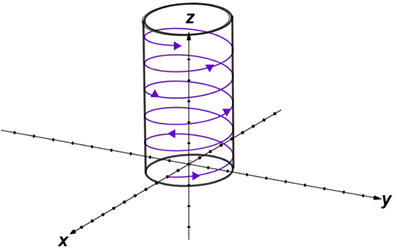
The cylinder shown above has a circular base with radius r on the xy-plane.
Did you know?
The structure of a DNA molecule is described as a double helix. This is because it looks like two helices (plural for helix) wrapping around each other.