Tessellation
A tessellation is a pattern of shapes repeated to fill a plane. The shapes do not overlap and there are no gaps.



Tessellations are something we often see in quilts, carpets, floors, and more. In the figure below are three examples.

The shape that is repeated, or tessellated, is called a motif. The following are the motifs for the tessellations above.

Sum of angles at a vertex
For a tessellation composed of polygons, the sum of the angles formed at any vertex equals 360°.

For the tessellation above composed of squares to the left, the sum of the angles at a vertex are 90°+90°+90°+90°=360°. The angles at a vertex to the right are 120°+120°+120°=360°. This is true for any vertex in the tessellation.
Classifying tessellations
There are 3 types of tessellations.
Regular tessellation
A regular tessellation is made up of regular congruent polygons. There are only three tessellations that are composed entirely of regular, congruent polygons.



Semi-regular tessellations
A semi-regular tessellation is a tessellation that is composed of two or more regular polygons such that the arrangement of the polygons is the same for each vertex in the tessellation.
The pattern around each vertex is identical. We call this pattern the order of the vertex of the tessellation, and name it based on the number of sides of each regular polygon surrounding the vertex.
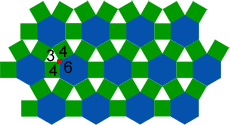
The order of the semi-regular tessellation composed of equilateral triangles, squares, and regular hexagons shown above is 3-4-6-4. Start with the polygon with the fewest number of sides first, then rotate clockwise or counterclockwise and count the number of sides for the successive polygons to complete the order.
There are only eight semi-regular tessellations.







Non-regular tessellations
A non-regular tessellation is a tessellation that is composed of other shapes that may or may not be polygons.

