Sector

A sector is a part of a circle enclosed by two radii and an arc. In the figure below are three sectors of a circle.

We see sectors all around us in our everyday lives. A slice of pizza is a sector; a window pane divides a circular window into sectors.

Properties of a sector

A sector of a circle is defined by the region bounded by two radii (plural for radius) of a circle and the arc they intercept.

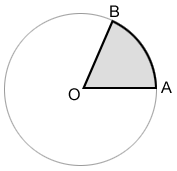
In the circle with center O above, sector AOB, shaded in gray, is bounded by radii OA and OB, and arc AB.

Central angles and sectors

A central angle is an angle whose vertex is the center of a circle. The two sides of a central angle are radii of the circle. The central angle is subtended by an arc, creating the sector of the circle.

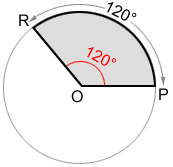
An important property in determining the area of a central angle is the relationship of the arc and its subtended angle. The measure of a central angle and the arc it subtends are equal. In the diagram above, central angle POR, which is subtended by arc PR, both have a measure of 120°.

Area with central angle in degrees

The area, A, of a circle with radius r is A = πr². Since a sector is a part of a circle, we can find its area as a fractional portion of the area of a circle.

where r is the radius and θ is the central angle in degrees.

Area with central angle in radians

If the central angle is measured in radians, the area of a sector is:

where r is the radius and θ is the central angle in radians.

Area with arc length

If the arc length, s, and radius, r, of the sector are known. The sector area is: