Concentric
In geometry, the term concentric describes the relationship between two or more objects that share the same center. Circles, spheres, regular polygons, and regular polyhedra can be concentric to each other if they share the same center.

A cross section of an onion shows a set of concentric circles. A whole onion is composed by layers of concentric spheres. Peeling a layer of the onion removes one of the spheres.
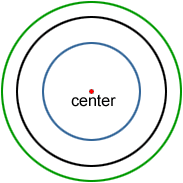
Concentric circles
Two circles are concentric if they share the same center and have different radii.
Concentric spheres
Concentric or homocentric spheres are spheres sharing the same center.
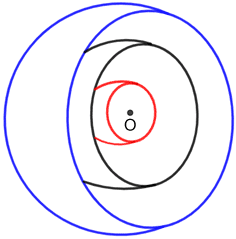
Above is a cross section of three concentric spheres that share their center at point O. Concentric spheres were used by Eudoxus and Aristotle to explain a cosmological model of the universe with the Earth at the center mathematically.
Concentric polygons
Concentric polygons are regular polygons that share the same center.
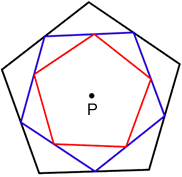
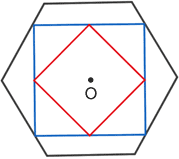
Concentric polygons do not need to have the same number of sides, they only need to be regular polygons and share the same center. In the figure below, two squares and a regular hexagon are concentric. They share the same center point, O.
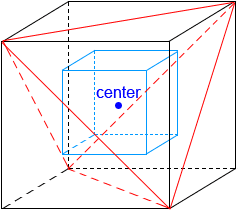
Concentric polyhedra
Concentric polyhedra are regular polyhedra that share the same center. Like concentric polygons, polyhedra do not need to have the same number of sides to be concentric. As long as the polyhedra share the same center and they are regular polyhedra, they are concentric. The figure below shows two cubes and a regular tetrahedron that are concentric.